| Расчетные сопротивления арматуры растяжению для основных видов стержневой и проволочной арматуры приведены в табл. 11 и 12.
Таблица 11
|
Стержневая арматура |
Расчетные сопротивления арматуры
для предельных состояний первой группы, МПа (кгс/см2) |
|
класса |
растяжению |
сжатию |
|
|
продольной Rs |
поперечной (хомутов и отогнутых стержней) Rsw |
продольной Rsc |
|
A-I |
225 (2300) |
Rsw gsw8 |
225 (2300) |
|
A-II |
280 (2850) |
(см. табл. 13) |
280 (2850) |
|
A-III диаметром, мм: |
|
|
|
|
6-8 |
355 (3600) |
|
355 (3600) |
|
10-20 |
365 (3750) |
|
365 (3750) |
|
A-IV |
510 (5200) |
|
400 (4000) |
|
A-V |
680 (6950) |
|
400 (4000) |
|
A-VI |
815 (8300) |
|
400 (4000) |
|
A-IIIв с контролем: |
|
|
|
|
удлинения и
напряжения |
490 (5000) |
|
200 (2000) |
|
только удлинения |
450 (4600) |
|
200 (2000) |
П р и м е ч а н и я: 1. В сварных каркасах для хомутов из арматуры класса А-III, диаметр которых меньше 1/3 диаметра продольных стержней, значения Rsw принимаются равными 255 МПа (2600 кгс/см2).
2. Расчетные сопротивления растянутой поперечной арматуры и сжатой продольной принимаются с учетом коэффициентов, указанных в пп. 2.23, 2.24 и табл. 13.
Таблица 12
|
Проволочная |
Диа- |
Расчетные сопротивления арматуры для предельных состояний первой группы, МПа (кгс/см2) |
|
арма- |
метр, |
растяжению |
сжатию |
|
тура класса |
мм |
продольной Rs |
поперечной (хомутов и отогнутых стержней) Rsw |
Rsc |
|
Вр-I |
3
4
5 |
375 (3850)
365 (3750)
360 (3700) |
Rsw gsw
(см. табл. 13) |
375 (3850)
365 (3750)
360 (3700) |
|
В-II |
3
4
5
6
7
8 |
1240 (12650)
1180 (12000)
1110 (11300)
1050 (10600)
980 (10000)
915 (93000) |
|
400 (4000)
400 (4000)
400 (4000)
400 (4000)
400 (4000)
400 (4000) |
|
Вр-II |
3
4
5
6
7
8 |
1215 (12400)
1145 (11700)
1045 (10700)
980 (10000)
915 (9300)
850 (8700) |
|
400 (4000)
400 (4000)
400 (4000)
400 (4000)
400 (4000)
400 (4000) |
Таблица 13
|
Арматура |
Расчетные сопротивления растяжению поперечной Rsw
и сжатой Rsc арматуры, МПа (кгс/см2),
при классе ячеистого бетона по прочности на сжатие |
|
В1 |
В1,5 |
В2 |
В2,5 |
В3,5 |
В5 |
В7,5 |
В10 |
В12,5 |
В15 |
|
Попереч-ная |
25
255 |
37,5
380 |
50
510 |
62,5
640 |
87,5
900 |
125
1270 |
187,5
1900 |
250
2550 |
310
3200 |
375
3800 |
|
Сжатая продоль-ная |
230
2350 |
250
2550 |
270
2750 |
295
3000 |
340
3450 |
390
4000 |
390
4000 |
390
4000 |
390
4000 |
390
4000 | П р и м е ч а н и я: 1. Над чертой даны классы бетона по прочности и расчетные сопротивления, МПа; под чертой - расчетные сопротивления, кгс/см2.
2. Расчетные сопротивления арматуры даны с учетом коэффициентов условий ее работы в бетоне классов В15 и ниже:
для сжатой арматуры gs8 = 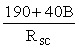 Ј 1 ; Ј 1 ;
" поперечной " gs8 = 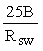 Ј 1 . Ј 1 .
2.23. Расчетные сопротивления арматуры сжатию Rsc, используемые при расчете конструкций по предельным состояниям первой группы, принимаются по табл. 11 и 12 с учетом коэффициентов условий работы gs9 по табл. 14 и не более величин, указанных в табл. 13.
Таблица 14 (27)
|
Защитное покрытие |
Коэффициент условий
работы gs9 при арматуре |
|
|
гладкой |
периодического профиля |
|
1. Цементно-полистирольное или латексно-минеральное |
1 |
1 |
|
2. Цементно-битумное (холодное) при диаметре арматуры, мм: |
|
|
|
св. 6 |
0,7 |
1 |
|
до 6 |
0,7 |
0,7 |
|
3. Битумно-силикатное (горячее) |
0,7 |
0,7 |
|
4. Битумно-глинистое |
0,5 |
0,7 |
|
5. Сланцебитумное, цементное |
0,5 |
0,5 |
2.24. Расчетные сопротивления поперечной арматуры в конструкциях из ячеистого бетона при работе их по наклонным сечениям на действие поперечной силы и изгибающего момента принимаются по табл. 13.
2.25. Длина передачи напряжения lо для напрягаемой арматуры двухслойных конструкций определяется согласно п. 2.29 СНиП 2.03.01-84.
2.26 (2.30). Значения модуля упругости арматуры Es принимаются по табл. 15.
Таблица 15 (29)
|
Класс арматуры |
Модуль упругости арматуры Еs Ч 10-4, МПа (кгс/см2) |
|
A-I, A-II |
21 (210) |
|
А-III |
20 (200) |
|
A-IV, A-V, A-VI |
19 (190) |
|
A-IIIв |
18 (180) |
|
Вр-I |
17 (170) |
|
В-II, Вр-II |
20 (200) |
3. РАСЧЕТ ЭЛЕМЕНТОВ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ИЗ ЯЧЕИСТЫХ БЕТОНОВ
ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ
РАСЧЕТ БЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ
3.1 (3.1). Расчет по прочности бетонных элементов должен производиться для сечений, нормальных к их продольной оси. В зависимости от условий работы элементов они рассчитываются без учета, а также с учетом сопротивления бетона растянутой зоны.
Без учета сопротивления бетона растянутой зоны производится расчет внецентренно сжатых элементов, указанных в п. 1.7а СНиП 2.03.01-84, принимая, что достижение предельного состояния характеризуется разрушением сжатого бетона.
Сопротивление бетона сжатию условно представляется напряжениями, равными Rb, равномерно распределенными по части сжатой зоны сечения - условной сжатой зоне (черт. 1) - сокращенно, именуемой в дальнейшем сжатой зоной бетона.
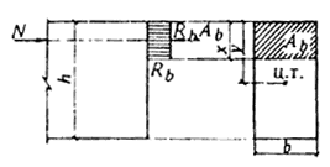
Черт. 1. Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси внецентренно сжатого бетонного элемента, рассчитываемого по прочности без учета сопротивлений бетона растянутой зоны
С учетом сопротивления бетона растянутой зоны производится расчет элементов, указанных в п. 1.7б СНиП 2.03.01-84, принимая, что достижение предельного состояния характеризуется разрушением бетона растянутой зоны (появлением трещин).
Предельные усилия определяются исходя из следующих предпосылок:
сечения после деформаций остаются плоскими;
наибольшее относительное удлинение крайнего растянутого волокна бетона равно 2Rbt/Eb;
напряжения в бетоне сжатой зоны определяются с учетом упругих (а в некоторых случаях и неупругих) деформаций бетона;
напряжения в бетоне растянутой зоны распределены равномерно и равны Rbt.
Кроме того, должен производиться расчет бетонных элементов на местное действие нагрузки (смятие) согласно п. 3.30.
Внецентренно сжатые элементы
3.2 (3.2). При расчете внецентренно сжатых бетонных элементов должен приниматься во внимание случайный эксцентриситет продольного усилия еа, определяемый согласно указаниям п. 1.18.
3.3 (3.3). При гибкости элементов lo/i > 14 необходимо учитывать влияние на их несущую способность прогибов в плоскости эксцентриситета продольного усилия и в нормальной к ней плоскости путем умножения значений ео на коэффициент h (см. п. 3.6).
В случае расчета из плоскости эксцентриситета продольного усилия значение ео принимается равным значению случайного эксцентриситета.
Применение внецентренно сжатых бетонных элементов не допускается при эксцентриситетах приложения продольной силы с учетом прогибов еоh, превышающих:
а) в зависимости от сочетания нагрузок:
при основном сочетании - 0,9 у,
« особом « - 0,95 y,
б) в зависимости от класса бетона по прочности: (у - 2).
Здесь у - расстояние от центра тяжести сечения до наиболее сжатого волокна бетона, см.
3.4 (3.4). Во внецентренно сжатых бетонных элементах в случаях, указанных в п. 5.48 СНиП 2.03.01-84, необходимо предусматривать конструктивную арматуру.
3.5 (3.5). Расчет внецентренно сжатых бетонных элементов (см. черт. 1) должен производиться из условия
N Ј a Rb Ab , (1)
где Аb - площадь сечения сжатой зоны бетона, определяемая из условия, что ее центр тяжести совпадает с точкой приложения равнодействующей внешних сил.
Для элементов прямоугольного сечения Ab определяется по формуле
Ab = bh 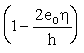 . (2) . (2)
Внецентренно сжатые бетонные элементы, в которых появление трещин не допускается по условиям эксплуатации (черт. 2) независимо от расчета из условия (1), должны быть проверены с учетом сопротивления бетона растянутой зоны (см. п. 3.1) из условия
N Ј 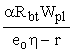 . (3) . (3)
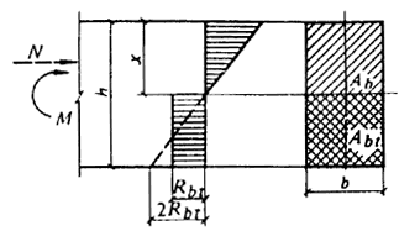
Черт. 2. Схема усилий и эпюра напряжений в сечении, нормальном
к продольной оси изгибаемого (внецентренно сжатого) бетонного
элемента, рассчитываемого по прочности с учетом сопротивления
растянутой зоны бетона
Для элементов прямоугольного сечения условие (3) имеет вид
N Ј 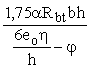 . (4) . (4)
В формулах (1) - (4):
h - коэффициент, определяемой по формуле (9);
a - коэффициент, принимаемый равным:
для автоклавных ячеистых бетонов - 0,85;
« неавтоклавных « - 0,75;
Wpl - момент сопротивления сечения для крайнего растянутого волокна с учетом неупругих деформаций растянутого бетона, определяемый в предположении отсутствия продольной силы по формуле
Wpl = 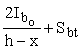 ; (5) ; (5)
j = 1,6 - 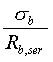 , (6) , (6)
r - расстояние от центра тяжести сечения до ядровой точки, наиболее удаленной от растянутой зоны, определяемое по формуле
r = j 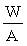 ; (7) ; (7)
положение нулевой линии определяется из условия
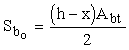 ; (8) ; (8)
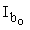 - момент инерции площади сечения сжатой зоны бетона относительно нулевой линии; - момент инерции площади сечения сжатой зоны бетона относительно нулевой линии;
Sbo и Sbt - статический момент площади сечения соответственно сжатой и растянутой зон бетона относительно нулевой линии;
х - высота сжатой зоны бетона.
3.6 (3.6). Значение коэффициента h, учитывающего влияние прогиба на эксцентриситет продольного усилия eо, следует определять по формуле
h = 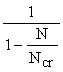 , (9) , (9)
где Ncr - условная критическая сила, определяемая по формуле
Ncr = 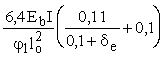 , (10) , (10)
где jl - коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента в предельном состоянии, равный
jl = l + b 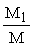 , (11) , (11)
но не более l + b.
Здесь b - коэффициент, принимаемый в зависимости от вида ячеистого бетона равным: для автоклавного - 1,3, для неавтоклавного - 1,5;
Ml - момент относительно растянутой или наименее сжатой грани сечения от действия постоянных и длительных нагрузок;
М - то же, от действия постоянных, длительных и кратковременных нагрузок;
lо - расчетная длина элемента, определяемая по табл. 16;
de - коэффициент, принимаемый равным eo/h, но не менее величины
de,min = 0,5 - 0,01 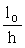 - 0,01 Rb , (12) - 0,01 Rb , (12)
где Rb принимается в МПа.
Если изгибающие моменты (или эксцентриситеты) от полной нагрузки и от суммы постоянных и длительных нагрузок имеют разные знаки, то при абсолютном значении эксцентриситета полной нагрузки еo, превышающем 0,1 h, принимают jl = 1; если это условие не удовлетворяется, значение jl принимается равным jl = jl1 + 10(l - jl1) 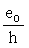 , где jl1 определяют по формуле (11), принимая М равным произведению продольной силы N на расстояние от центра тяжести сечения до соответствующей грани сечения. , где jl1 определяют по формуле (11), принимая М равным произведению продольной силы N на расстояние от центра тяжести сечения до соответствующей грани сечения.
При расчете бетонных элементов, имеющих несмещаемые опоры, значения коэффициента h принимаются для сечения в средней трети длины элемента по формуле (9), а для сечений в пределах крайних третей длины элемента - путем линейной интерполяции, принимая в опорных сечениях значения h равными единице.
Таблица 16
|
Характер опирания элементов |
Расчетная длина lo |
|
Для стен, опирающихся вверху и внизу: |
|
|
а) при шарнирах на двух концах, независимо от величины смещения опор |
Н |
|
б) при защемлении одного из концов и возможном смещении опор: |
|
|
для многопролетных зданий |
1,25 Н |
|
« однопролетных « |
1,5 Н |
П р и м е ч а н и е. Н - высота стены в пределах этажа за вычетом толщины плиты перекрытия.
3.7. Расчет сжатых бетонных элементов (при косом внецентренном сжатии) производится по формуле (1), при этом:
а) площадь сечения сжатой зоны бетона Аb условно принимается в виде прямоугольника, центр тяжести которого совпадает с точкой приложения силы и две стороны ограничены контуром сечения элемента (черт. 3), при этом
bc = 2Cb = 2 (yb - eoy) , (13)
hc = 2Ch = 2 (yh - eox) . (14)
В формулах (13) и (14):
Cb и Сh - расстояния от точки приложения силы до ближайших границ сечения.
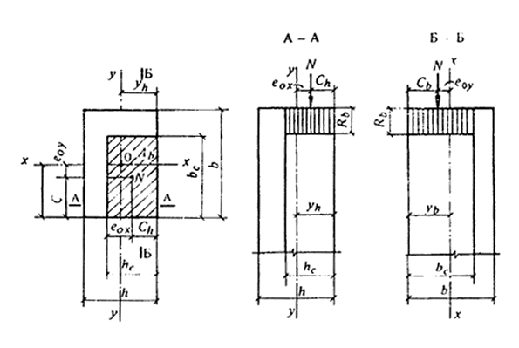
Черт. 3. Схема расположения усилий и эпюра напряжений в поперечном сечении бетонного элемента при косом внецентренном сжатии
Площадь условной сжатой зоны бетона равна:
Ab = 4 (yh - eox) (yb - eoy) ; (15)
б) влияние продольного изгиба учитывается в соответствии с п. 3.6, при этом величины h и d опредеыяются в двух вариантах:
1) при высоте сечения h и эксцентриситете еох - в направлении h;
2) при высоте сечения h = b и эксцентриситете eoy - в направлении b.
При двух вариантах значения h за расчетную несущую способность принимается меньшая из значений, вычисленных по формуле (1). Проверка несущей способности с учетом сопротивления бетона растянутой зоны и соответствующем направлении производится по формулам (3) и (4).
3.8 (3.7). Расчет элементов бетонных конструкций на местное сжатие (смятие) следует выполнять согласно пп. 3.30.- 3.31.
Расчет опорных сечений сжатых элементов конструкций в зонах, примыкающих к горизонтальным растворным швам, производится в соответствии с прил. 4.
Изгибаемые элементы
3.9 (3.8). Расчет изгибаемых бетонных элементов (см. черт. 2) должен производиться из условия
M Ј a Rbt Wpl, (16)
где a - коэффициент, принимаемый согласно п. 3.5;
Wpl - определяется по формуле (5); для элементов прямоугольного сечения принимается равным:
Wpl = 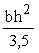 . (17) . (17)
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ
3.10. Расчет по прочности элементов железобетонных конструкций должен производиться для сечений, нормальных и наклонных к их продольной оси. При необходимости должен производиться расчет на местное смятие.
Расчет по прочности сечений,
нормальных к продольной оси элемента
3.11 (3.10). Предельные усилия в сечении, нормальном к продольной оси элемента, следует определять исходя из следующих предпосылок:
сопротивление бетона растяжению принимается равным нулю;
сопротивление бетона сжатию представляется напряжениями, равными Rb, равномерно распределенными по сжатой зоне бетона;
растягивающие напряжения в арматуре принимаются не более расчетного сопротивления растяжению Rs;
сжимающие напряжения в арматуре принимаются не более расчетного сопротивления сжатию Rsc.
При наличии в элементе напрягаемой и ненапрягаемой арматуры из стали различных видов и классов каждый вид и класс арматуры вводят в расчет прочности со своими расчетными сопротивлениями. В этом случае в расчетных формулах произведения RsAs и Rsc Asў заменяют суммой произведений расчетных сопротивлений каждого вида арматуры на соответствующие площади их сечений, а произведения RsSso и RscSsoў заменяют суммой произведений расчетных сопротивлений арматуры на статические моменты соответствующих площадей сечений арматуры.
Расчет двухслойных элементов по прочности при расположении слоя тяжелого бетона в растянутой зоне производится так же, как и для однослойных ячеистобетонных элементов; при расчете по деформациям прочность тяжелого бетона принимают равной его классу, указанному в проекте.
В таких элементах положение центра тяжести площади всего сечения бетона или его сжатой зоны, а также статические моменты следует определять, приводя все сечения к классу ячеистого бетона.
3.12 (3.11). Расчет сечений, нормальных к продольной оси элемента, когда внешняя сила действует в плоскости оси симметрии сечения и арматура сосредоточена у перпендикулярных к указанной плоскости граней элемента, следует производить в зависимости от соотношения между значением относительной высоты сжатой зоны бетона 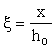 , определяемой из соответствующих условий равновесия, и значением относительной высоты сжатой зоны бетона (см. п. 3.13), при котором предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению Rs, с учетом соответствующих коэффициентов условий работы арматуры, за исключением коэффициента gs6 по п. 3.13 СНиП 2.03.01-84. , определяемой из соответствующих условий равновесия, и значением относительной высоты сжатой зоны бетона (см. п. 3.13), при котором предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению Rs, с учетом соответствующих коэффициентов условий работы арматуры, за исключением коэффициента gs6 по п. 3.13 СНиП 2.03.01-84.
3.13 (3.12). Значение xR определяется по формуле
xR = 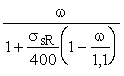 , (18) , (18)
где w = a - b Rb ;
a = 0,8;
b = 0,008;
Rb - принимается в МПа.
ssR - напряжение в арматуре, МПа, принимаемое равным для арматуры классов:
А-I, А-II, А-III, А-IIIв и Вр-I ssR = Rs - ssp ;
A-IV, A-V, A-VI ssR = Rs + 400 - ssp - Dssp ;
В-II, Вр-II ssR = Rs + 400 - ssp ;
здесь Rs - расчетное сопротивление арматуры растяжению с учетом соответствующих коэффициентов условий работы арматуры gsi , за исключением gs6 (см. п. 3.13 СНиП 2.03.01-84);
ssR - принимается при коэффициенте gsp < 1;
Dssp - см. п. 3.28 СНиП 2.03.01-84.
При этом xR должно быть не более 0,6.
3.14 (3.13). При расчете по прочности железобетонных элементов с высокопрочной арматурой классов A-IV, A-V, A-VI, В-II, Вр-II при соблюдении условия x Ј xR расчетное сопротивление арматуры Rs должно быть умножено на коэффициент условий работы gs6 , определяемый в соответствии с п. 3.13 СНиП 2.03.01-84.
Изгибаемые элементы прямоугольного сечения
3.15 (3.15). Расчет прямоугольных сечений изгибаемых элементов, указанных в п. 3.12 (черт. 4), при x = 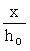 Ј xR должен производиться из условия: Ј xR должен производиться из условия:
М Ј Rb bx (ho - 0,5x) + Rsc Asў (ho - aў) , (19)
при этом высота сжатой зоны х определяется по формуле
Rs As - Rsc Asў = Rb bx , (20)
и принимается с учетом п. 3.16.
Расчет тавровых и двутавровых сечений производится в соответствии с п. 3.16 СНиП 2.03.01-84.
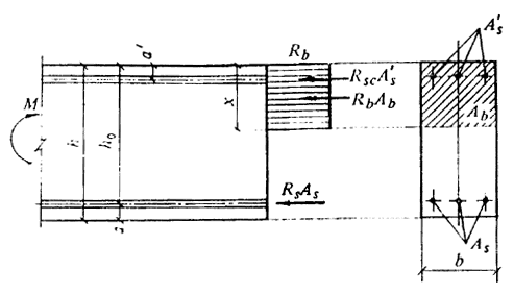
Черт. 4. Схема усилий и эпюра напряжении в сечении,
нормальном к продольной оси изгибаемого железобетонного элемента, при расчете его по прочности
3.16 (3.17). При расчете по прочности изгибаемых элементов рекомендуется соблюдать условие
х Ј xR ho . (21)
В случае, когда площадь сечения растянутой арматуры по конструктивным соображениям или из расчета по предельным состоянием второй группы принята большей, чем это требуется для соблюдения условия х Ј xR ho, расчет следует производить по формулам для общего случая (см. п. 3.21).
Если полученное из расчета по формуле (20) значение х > xR ho, допускается производить расчет из условия (19), определяя высоту сжатой зоны из формулы
ss As - Rsc Asў = Rb bx , (22)
где ss = 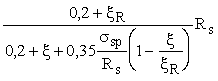 ; (23) ; (23)
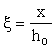 (x подсчитывается при значениях Rs с учетом соответствующих коэффициентов условий работы арматуры); (x подсчитывается при значениях Rs с учетом соответствующих коэффициентов условий работы арматуры);
ss - определяется при коэффициенте gsp, большем единицы.
Для элементов с ненапрягаемой арматурой классов А-I, А-II и А-III и Вр-I при х > xR ho допускается также производить расчет из условия (19), подставляя в него значение х = xR ho .
Внецентренно сжатые элементы прямоугольного сечения
3.17 (3.19). При расчете внецентренно сжатых железобетонных элементов необходимо учитывать случайный начальный эксцентриситет, согласно п. 1.18, а также влияние прогиба на их несущую способность в соответствии с п. 3.19.
3.18 (3.20). Расчет прямоугольных сечений внецентренно сжатых элементов, указанных в п. 3.12, следует производить:
а) при x = 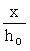 і xR (черт. 5) - из условия і xR (черт. 5) - из условия
Ne Ј Rb bx (ho - 0,5x) + Rsc Asў (ho - aў) , (24)
при этом высота сжатой зоны определяется из формулы
N + Rs As - Rsc Asў = Rb bx , (25)
б) при x = 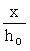 > xR - также из условия (24); > xR - также из условия (24);
при этом высота сжатой зоны определяется:
для элементов с ненапрягаемой арматурой классов А-I, A-II, A-III - из формулы
N + ss As - Rsc Asў = Rb bx , (26)
где ss = 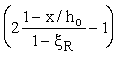 Rs ; (27) Rs ; (27)
для элементов с арматурой классов выше А-III (ненапрягаемой и напрягаемой) - из формул (30) - (32).
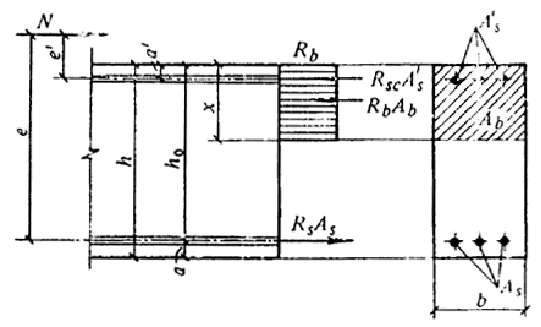
Черт. 5. Схема и эпюра напряжения в сечении, нормальном
к продольной оси внецентренно сжатого железобетонного элемента,
при расчете его по прочности
3.19 (3.24). При расчете внецентренно сжатых элементов следует учитывать влияние прогиба на их несущую способность, как правило, путем расчета конструкций по деформированной схеме (см. п. 1.15 СНиП 2.03.01-84). Допускается производить расчет конструкций по недеформированной схеме, учитывая при гибкости 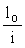 > 14 влияние прогиба элемента на его прочность, определяемую из условий (24) и (29) путем умножения ео на коэффициент h. > 14 влияние прогиба элемента на его прочность, определяемую из условий (24) и (29) путем умножения ео на коэффициент h.
При этом условная критическая сила в формуле (9) для вычисления h определяется по формуле
Ncr = 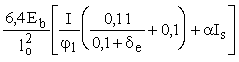 , (28) , (28)
где lо - принимается в соответствии с п. 3.20;
de - коэффициент, принимаемый согласно п. 3.6;
jl - коэффициент, определяемый по формуле (11); при этом моменты М и Мl определяются относительно оси, параллельной линии, ограничивающей сжатую зону и проходящей через центр наиболее растянутого или наименее сжатого (при целиком сжатом сечении) стержня арматуры, соответственно от действия полной нагрузки и от действия постоянных и длительных нагрузок. Если изгибающие моменты (или эксцентриситеты) от действия полной нагрузки и от действия постоянных и длительных нагрузок имеют разные знаки, следует учитывать указания п. 3.6.
При расчете из плоскости действия изгибающего момента эксцентриситет продольной силы ео принимается равным величине случайного эксцентриситета (см. п. 1.18).
3.20 (3.25). Расчетные длины lо внецентренно сжатых железобетонных элементов рекомендуется определять как для элементов рамной конструкции с учетом ее деформированного состояния при наиболее невыгодном для данного элемента расположении нагрузки, принимая во внимание неупругие деформации материалов и наличие трещин по табл. 16.
Общий случай расчета при любых сечениях, внешних усилиях
и любом армировании
3.21 (3.28). Расчет сечений в общем случае (черт. 6) должен производиться из условия
М Ј Rb Sb - S ssi Ssi . (29)
В условии (29):
М - в изгибаемых элементах - проекция момента внешних сил на плоскость, перпендикулярную прямой, ограничивающей сжатую зону сечения; во внецентренно сжатых элементах - момент продольной силы N относительно оси, параллельной прямой, ограничивающей сжатую зону и проходящей через центр тяжести сечения наиболее растянутого или наименее сжатого стержня продольной арматуры;
Sb и Ssi - статические моменты площади сечения сжатой зоны бетона и i-го стержня продольной арматуры относительно соответствующей из указанных выше осей (в изгибаемых элементах положение этой оси принимается таким же, как и во внецентренно сжатых);
ssi - напряжение в i-м стержне продольной арматуры, определяемое согласно указаниям настоящего пункта.
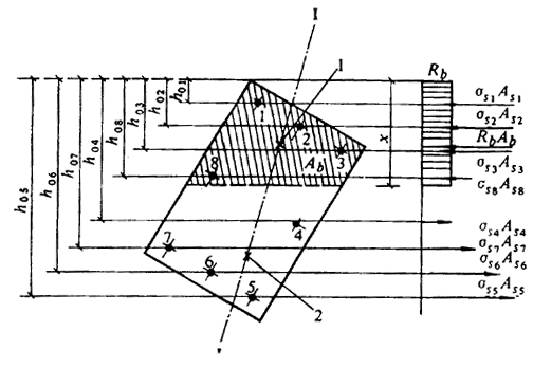
Черт. 6. Схема усилий и эпюра напряжений в сечении, нормальном
к продольной оси железобетонного элемента,
в общем случае расчета по прочности
I-I - плоскость, параллельная плоскости действия изгибающего момента
1 - точка приложения равнодействующей усилий в сжатой арматуре и в бетоне сжатой зоны; 2 - точка приложения равнодействующей усилий в растянутой арматуре
Высота сжатой зоны х и напряжение ssi определяются из совместного решения уравнений:
Rb Ab - S ssi Asi - N = 0 ; (30)
ssi = 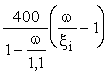 + sspi . (31) + sspi . (31)
В формулах (30) и (31) :
sspi - предварительное напряжение в i-м стержне продольной арматуры, принимаемое при коэффициенте gsp, назначаемом в зависимости от расположения стержня.
Asi - площадь сечения i-гo стержня продольной арматуры;
xi - относительная высота сжатой зоны бетона,
xi = 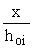 , ,
где hoi - расстояние от оси, проходящей через центр тяжести сечения рассматриваемого i-го стержня арматуры и параллельной прямой, ограничивающей сжатую зону до наиболее удаленной точки сжатой зоны сечения (см. черт. 6);
w - характеристика сжатой зоны ячеистого бетона, определяемая по формуле (18);
Кроме того, для определения положения границы сжатой зоны при косом изгибе требуется соблюдение дополнительного условия параллельности плоскости действия моментов внешних и внутренних сил, а при косом внецентренном сжатии - условия, чтобы точки приложения внешней продольной силы, равнодействующей сжимающих усилий в бетоне и арматуре и равнодействующей усилий в растянутой арматуре, лежали на одной прямой (см. черт. 6).
Если значение ssi, полученное по формуле (30), для арматуры классов A-IV, A-V, B-II, Bp-II превышает bRsi, то напряжение ssi следует определять по формуле
ssi = 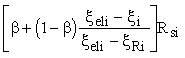 , (32) , (32)
где xRi и xeli - относительная высота сжатой зоны, отвечающая достижению в рассматриваемом стержне напряжений, соответственно равных Rsi и bRsi , значения xRi и xeli определяются по формуле
xRi(eli) = 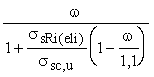 . (33) . (33)
Здесь ssRi = Rsi + 400 - sspi - Dsspi , МПа - при определении xRi ;
ss,eli = b Rsi - sspi , МПа - при определении xeli ;
ssc,u - см. п. 3.22 СНиП 2.03.01-84.
Значения Dsspi и коэффициента b принимаются в соответствии с п. 3.28 СНиП 2.03.01-84.
В случае, когда напряжение в арматуре, найденное по формуле (32), превышает Rsi без учета коэффициента gs6, в условия (29) и (30) подставляется значение ssi, равное Rsi, с учетом соответствующих коэффициентов условий работы, в том числе gs6 (см. п. 3.13 СНиП 2.03.01-84).
Напряжение ssi вводится в расчетные формулы со своим знаком, полученным при расчете по формулам (31) и (32), при этом необходимо соблюдать следующие условия:
во всех случаях Rsi і ssi і -Rsci ;
для предварительно напряженных элементов ssi і ssci , здесь ssci - напряжение в арматуре, равное предварительному напряжению sspiў, уменьшенному на величину ssc,u (см. пп. 3.12, 3.22 СНиП 2.03.01-84) .
Расчет по прочности сечений,
наклонных к продольной оси элемента
3.22 (3.29). Расчет железобетонных элементов из ячеистых бетонов по наклонным сечениям должен производиться для обеспечения прочности:
на действие поперечной силы по наклонной полосе между наклонными трещинами (п. 3.23);
на действие поперечной силы по наклонной трещине (п. 3.24) ;
на действие изгибающего момента по наклонной трещине (п. 3.26).
3.23 (3.30). Расчет железобетонных элементов на действие поперечной силы для обеспечения прочности по наклонной полосе между наклонными трещинами должен производиться из условия
Q Ј 0,3 jw1 jb1 Rb bho . (34)
Коэффициент jw1, учитывающий влияние хомутов, нормальных к продольной оси элемента, определяется по формуле
jw1 = 1 +5 a mw , но не более 1,3 , (35)
где 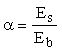 ; ; 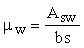 ; ;
s - расстояние между хомутами, измеренное по нормали к ним.
Коэффициент jb1 определяется по формуле
jb1 = 1 - 0,01 Rb , (36)
где Rb - в МПа.
3.24 (3.31). Расчет железобетонных элементов из ячеистых бетонов с поперечной арматурой (черт. 7) на действие поперечной силы для обеспечения прочности по наклонной трещине должен производиться по наиболее опасному наклонному сечению из условия
Q Ј Qb + Qsw + Qs,inc . (37)
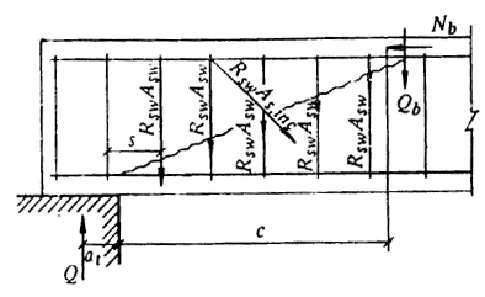
Черт. 7. Схема усилий в сечении, наклонном к продольной оси
железобетонного элемента, при расчете его по прочности
на действие поперечной силы
Поперечная сила Q в условии (37) определяется от внешней нагрузки, расположенной но одну сторону от рассматриваемого наклонного сечения.
Поперечное усилие Qb , воспринимаемое бетоном, определяется по формуле
Qb = 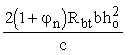 , (38) , (38)
где c - длина проекции наиболее опасного наклонного сечения на продольную ось элемента.
Коэффициент jn , учитывающий влияние продольных сил, определяется по формуле:
при действии продольных сжимающих сил
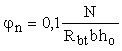 , но не более 0,5. (39) , но не более 0,5. (39)
Для предварительно напряженных элементов в формулу (39) вместо N подставляется усилие предварительного обжатия Р; положительное влияние продольных сжимающих сил не учитывается, если они создают изгибающие моменты, одинаковые по знаку с моментами от действия поперечной нагрузки; значение 1 + jn во всех случаях принимается не более 1,5.
Значение Qb, вычисленное по формуле (38), принимается не менее величины 0,6 (1 + jn) Rbt bho.
При расчете железобетонных элементов с поперечной арматурой должна быть также обеспечена прочность по наклонному сечению в пределах участка между хомутами, опорой и отгибом и отгибами (черт. 8).
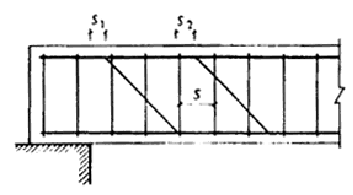
Черт. 8. Расстояния между хомутами и отогнутыми стержнями
Поперечные усилия Qsw и Qs,inc определяются как сумма проекций на нормаль к продольной оси элемента предельных усилий соответственно в хомутах и отгибах, пересекающих опасную наклонную трещину.
Длина co проекции опасной наклонной трещины на продольную ось элемента определяется из минимума выражения Qb + Qsw + Qs,inc, где в значение Qb вместо с подставляется co; полученное значение со принимается не более 2ho и не более значения с, а также не менее ho, если с > hо.
Для элементов с поперечной арматурой в виде хомутов, нормальных к продольной оси элемента и имеющих постоянный шаг в пределах рассматриваемого наклонного сечения, значение со соответствует минимуму усилия Qb + Qsw и определяется по формуле
co = 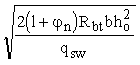 , (40) , (40)
где qsw - усилие в хомутах на единицу длины элемента, определяемое по формуле
qsw = 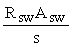 . (41) . (41)
Для таких элементов поперечное усилие Qsw определяется по формуле
Qsw = qsw co . (42)
При этом для хомутов, устанавливаемых по расчету, следует соблюдать условие
qsw і 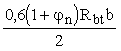 . (43) . (43)
Кроме того, поперечная арматура должна удовлетворять требованиям пп. 5.12-5.17.
3.25 (3.32). Расчет железобетонных элементов без поперечной арматуры на действие поперечной силы для обеспечения прочности по наклонной трещине должен производиться по наиболее опасному наклонному сечению из условия
Q Ј 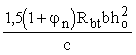 , (44) , (44)
где правая часть условия (44) принимается не более 2,5Rbtbho и не менее 0,6 (1 + jn) Rbt bho .
Коэффициент jn определяется согласно п. 3.24.
3.26 (3.35). Расчет железобетонных элементов на действие изгибающего момента (черт. 9) для обеспечения прочности по наклонной трещине должен производиться по опасному наклонному сечению из условия
М Ј Мs + Msw + Ms,inc . (45)
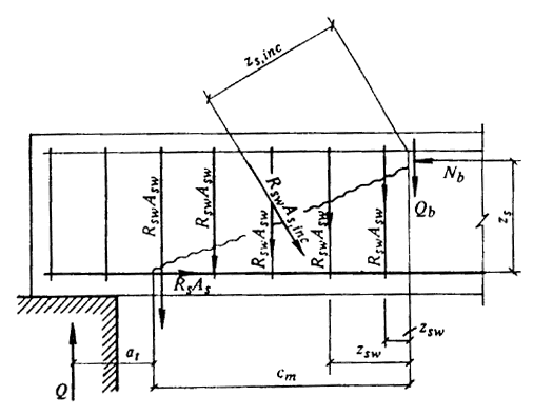
Черт. 9. Схема усилий в сечении, наклонном к продольной оси
железобетонного элемента, при расчете его по прочности
на действие изгибающего момента
Момент М в условии (45) определяется от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения относительно оси, перпендикулярной плоскости действия момента и проходящей через точку приложения равнодействующей усилий Nb в сжатой зоне.
Моменты Мs, Мsw и Мs,inc определяются соответственно как сумма моментов относительно той же оси от усилий в продольной арматуре в хомутах и отогнутых стержнях, пересекающих растянутую зону наклонного сечения, и вычисляются по формулам:
Ms = Rs As zs ; (46)
Msw = S Rsw Asw zsw ; (47)
Ms,inc = S Rs,inc As,inc zs,inc , (48)
где zs, zsw и zs,inc - расстояния от плоскостей расположения соответственно продольной арматуры, хомутов и отогнутых стержней до указанной выше оси.
Высота сжатой зоны наклонного сечения определяется из условия равновесия проекций усилий в бетона сжатой зоны и в арматуре, пересекающей растянутую зону наклонного сечения на продольную ось элемента.
Расчет наклонных сечений на действие момента производится в приопорных участках и местах резкого изменения размеров элементов (подрезки, узлы и т.д.), а также в местах обрыва или отгиба продольной арматуры.
Для конструкций из ячеистых бетонов усилия в продольной арматуре за наклонной трещиной должны определяться по расчету только с учетом работы поперечных анкеров на приопорных участках.
Момент Мsw, воспринимаемый хомутами, нормальными к продольной оси элемента, с равномерным шагом в пределах растянутой зоны рассматриваемого наклонного сечения, определяется по формуле
Мsw = qsw 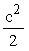 , (49) , (49)
где qsw - усилие в хомутах на единицу длины элемента, определяемое по формуле (41);
c - длина проекции опасного наклонною сечения на продольную ось элемента.
3.27. Концы продольной арматуры железобетонных элементов должны быть заанкерены (см. п. 3.35 СНиП 2.03.01-84). Анкеровка продольной арматуры железобетонных конструкций из ячеистых бетонов определяется расчетом.
Значение расчетного усилия Nan, воспринимаемого анкерными поперечными стержнями, приваренными к продольным стержням ненапрягаемой арматуры в однородных элементах, вычисляется по формуле
Nan = 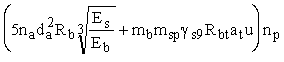 , (50) , (50)
где na - число анкерных поперечных стержней, принимаемое с учетом п. 5.10;
da - диаметр анкерных поперечных стержней, см;
mb - коэффициент, учитывающий вид бетона; принимается: для автоклавных - 1; для неавтоклавных - 0,9;
msp - коэффициент, учитывающий вид арматуры; принимается: для гладкой арматуры - 2; для арматуры периодического профиля - 2,5;
gs9 - коэффициент, учитывающий вид антикоррозионной обмазки по табл. 14;
at - расстояние от оси опоры до первой наклонной трещины, определяемое согласно п. 3.28;
u - периметр продольного стержня;
np - число анкеруемых продольных стержней в поперечном сечении элемента.
П р и м е ч а н и я: 1. Число расчетных анкерных поперечных стержней, расположенных в одной плоскости, должно быть не более четырех, а расстояние между анкерными стержнями в свету не менее 50 мм.
2. В конструкциях балочного типа, армированных вертикальными каркасами (когда поперечные анкерные стержни расположены вертикально), величину расчетного усилия, воспринимаемого анкерами, определяют по формуле (50) настоящего Пособия и умножают его на коэффициент 0,6.
3. Усилие, воспринимаемое горизонтально расположенными анкерами, при условия соблюдения требований примеч. 1 принимают пропорционально их числу в том случае, если расстояние от начала наклонной трещины до оси близлежащего анкера не менее 100 мм. Если расстояние будет меньше 100 мм, но не менее 50 мм, усилие, воспринимаемое ближайшим к наклонной трещине анкером, умножают на коэффициент 0,6.
4. Усилия, воспринимаемый анкерами, приваренными к стержням, расположенным у боковой грани на расстоянии защитного слоя от нее, определяются по формуле (50) с введением коэффициента 0,5.
3.28. Начало наиболее опасного наклонного сечения принимают на расстоянии а, от оси опоры (см. черт. 9) и вычисляют по формуле
at = 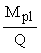 , (51) , (51)
где Mpl - момент появления трещин, определяемый с учетом сжатой и растянутой арматуры для опорного сечения по формуле (62);
Q - расчетная поперечная сила, определяемая в сечении на расстоянии at от опоры. Допускается принимать максимальное значение величины Q, соответствующее опорному сечению.
Конец наиболее опасного (по изгибающему моменту) наклонного сечения определяется проекцией длины этого сечения на продольную ось элемента (величиной cm), которую находят из уравнения
Q = S Rsw Asw = S Rsw As,inc sin q . (52)
При поперечных стержнях, равномерно распределенных вдоль оси элемента, проекцию длины наиболее опасного наклонного сечения на ось элемента с определяют по формуле
cm = 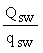 , (53) , (53)
где qsw - определяют по формуле (41).
При равномерно распределенной нагрузке конец наиболее опасного наклонного сечения должен располагаться не далее 1/4 пролета от оси опоры (т.е. аt + сm Ј 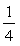 l) с тем, чтобы момент внешних сил М в формуле (45) не превышал максимального изгибающего момента l) с тем, чтобы момент внешних сил М в формуле (45) не превышал максимального изгибающего момента 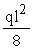 . .
При сосредоточенной нагрузке конец наиболее опасного наклонного сечения должен располагаться так, чтобы момент внешних сил в формуле (45) не превышал максимального изгибающего момента для данного элемента.
При отсутствии поперечной арматуры, устанавливаемой по расчету, момент внешних сил принимают равным максимальному изгибающему моменту.
3.29. Для двухслойных элементов должна быть проверена прочность по наклонным сечениям от сдвига слоя плотного бетона относительно слоя ячеистого бетона по формуле
N = at b Rbt , (54)
где b - ширина площади сопряжения двух слоев бетона в сечении элемента, в котором определяют прочность на сдвиг;
Rbt - расчетное сопротивление ячеистого бетона на растяжение, принимаемое по табл. 7 (в зависимости от его класса по прочности на сжатие, но не более 0,15 МПа (1,5 кгс/см2) .
Расчет железобетонных элементов на местное действие нагрузки
3.30 (3.39). При расчете на местное сжатие (смятие) элементов без поперечного армирования должно удовлетворяться условие
N Ј y Rb,loc Aloc1 , (55)
где N - продольная сжимающая сила от местной нагрузки;
y - коэффициент, зависящий от характера распределения местной нагрузки по площади смятия и принимаемый равным: при равномерном распределении местной нагрузки на площади смятия - 1,0; при неравномерном распределении местной нагрузки на площади смятия (под концами балок, прогонов, перемычек) - 0,5;
Alocl - площадь смятия;
Rb,loc - расчетное сопротивление ячеистого бетона смятию, определяемое по формуле
Rb,loc = jb Rb , (56)
здесь jb = 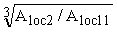 , (57) , (57)
но не более следующих значений: при схеме приложения нагрузки по черт. 10, а, в, г, е - 1,2; при схеме приложения нагрузки по черт. 10, б, д - 1,0;
Rb - принимается как для бетонных конструкций (см. п. 2.11 и табл. 6);
Аloc2 - расчетная площадь смятия, определяемая в соответствии с п. 3.31.
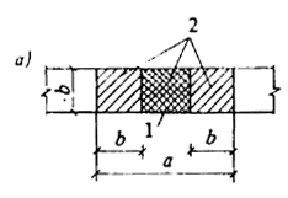
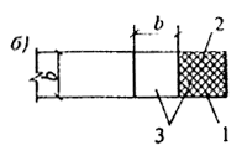
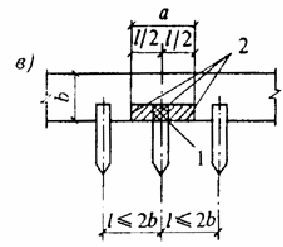
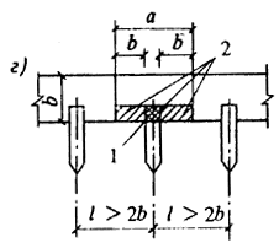

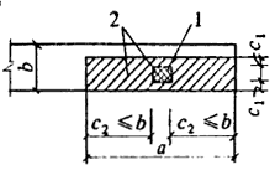
Черт. 10. Расчетные схемы, принятые при расчете на местное сжатие
а-е - различные случаи местного сжатия; 1 - площадь смятия; 2 - расчетная площадь смятия; 3 - расчетная площадь смятия, учитываемая только при наличии косвенной арматуры
3.31 (3.40). В расчетную площадь Аloc2 включается участок, симметричный по отношению к площади смятия (см. черт. 10). При этом должны выполняться следующие условия:
при местной нагрузке по всей ширине элемента b в расчетную площадь включается участок длиной не более b в каждую сторону от границы местной нагрузки (см. черт. 10, a);
при местной краевой нагрузке по всей ширине элемента расчетная площадь Aloc2 равна площади смятия Aloc1 (см. черт. 10, б);
при местной нагрузке в местах опирания концов прогонов и балок в расчетную площадь включается участок шириной, равной глубине заделки прогона или балки, и длиной не более расстояния между серединами пролетов, примыкающих к балке (см. черт. 10, в);
если расстояние между балками превышает двойную ширину элемента, длина расчетной площади определяется как сумма ширины балки и удвоенной ширины элемента (см. черт. 10, г) ;
при местной краевой нагрузке на угол элемента (см. черт. 10, д) расчетная площадь Aloc2 равна площади смятия Аloc1 ;
при местной нагрузке, приложенной на части длины и ширины элемента, расчетная площадь принимается согласно черт. 10, е. При наличии нескольких нагрузок указанного типа расчетные площади ограничиваются линиями, проходящими через середину расстояний между точками приложения двух соседних нагрузок.
П р и м е ч а н и е. При местной нагрузке от балок, прогонов, перемычек и других элементов, работающих на изгиб, учитываемая в расчете глубина опоры при определении Aloc1 и Aloc2 принимается не более 20 см.
4. РАСЧЕТ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ
КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ
ВТОРОЙ ГРУППЫ
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ
ПО ОБРАЗОВАНИЮ ТРЕЩИН
4.1. Железобетонные элементы из ячеистых бетонов рассчитываются по образованию трещин, нормальных к продольной оси элемента.
4.2. Расчет по образованию трещин железобетонных элементов из ячеистых бетонов производится в соответствии с пп. 4.2-4.9 СНиП 2.03.01-84.
При определении момента трещинообразования по формуле (125) СНиП 2.03.01-84 допускается определять момент сопротивления приведенного сечения по формуле
Wpl = g Wred , (58)
где g - коэффициент, принимаемый по табл. 3 прил. 3;
Wred - момент сопротивления приведенного сечения, определяемый по формуле
Wred = 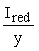 ; (59) ; (59)
здесь у - расстояние от центра тяжести приведенного сечения до растянутого краевого волокна;
Ired - приведенный момент инерции с учетом продольной напрягаемой и ненапрягаемой арматуры, который может быть определен по формуле
Ired = i 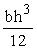 , (60) , (60)
где i - коэффициент, принимаемый по графикам черт. 1 и 2 прил. 3 в зависимости от коэффициентов:
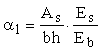 ; ; 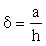 ; ; 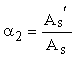 . (61) . (61)
Для однородных элементов прямоугольного сечения без предварительного напряжения момент трещинообразования может быть определен по формуле
Mpl = Wpl b h2 Rbt,ser , (62)
где Wpl - коэффициент, принимаемый по графикам черт. 3 и 4 прил. 3 в зависимости от характеристик армирования a2 и
a1ў = 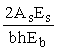 . (63) . (63)
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО РАСКРЫТИЮ НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ ТРЕЩИН
4.3. Железобетонные элементы из ячеистых бетонов рассчитываются по раскрытию трещин, нормальных к продольной оси элемента.
4.4 (4.14). Ширину раскрытия трещин, нормальных к продольной оси элемента acrс, мм, следует определять по формуле
acrc = jl h 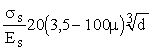 , (64) , (64)
где jl - коэффициент; принимаемый равным при учете:
кратковременных нагрузок и непродолжительного действия постоянных и длительных нагрузок - 1;
продолжительного действия постоянных и длительных нагрузок - 2,5;
h - коэффициент, принимаемый равным:
при стержневой арматуре периодического профиля - 1,0;
„ стержневой арматуре гладкой - 1,3;
„ проволочной арматуре периодического профиля - 1,2;
„ проволочной гладкой арматуре - 1,4;
ss - напряжение в стержнях крайнего ряда арматуры S или (при наличии предварительного напряжения) приращение напряжений от действия внешней нагрузки, определяемое согласно п. 4.5;
m - коэффициент армирования сечений, принимаемый равным отношению площади сечения арматуры S к площади сечения бетона (при рабочей высоте ho), но не более 0,02;
d - диаметр стержня арматуры, мм.
Для элементов, к трещиностойкости которых предъявляются требования 2-й категории, ширина раскрытия трещин определяется от суммарного действия постоянных, длительных и кратковременных нагрузок при коэффициенте jl = 1.
Для элементов, к трещиностойкости которых предъявляются требования 3-й категории, ширина продолжительного раскрытия трещин определяется от действия постоянных и длительных нагрузок при коэффициенте jl > 1. Ширина непродолжительного раскрытия трещин определяется как сумма ширины продолжительного раскрытия и приращения ширины раскрытия от действия кратковременных нагрузок, определяемых при коэффициенте jl = 1.
Ширина раскрытия трещин, определенная по формуле (64), корректируется в следующих случаях:
а) если центр тяжести сечения стержней крайнего ряда арматуры S изгибаемых, внецентренно сжатых элементов при еo,tot і 0,8ho отстоит от наиболее растянутого волокна на расстоянии а2, большем 0,2h, значение аarc должно быть увеличено путем умножения на коэффициент da, равный
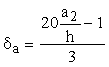 (65) (65)
и принимаемый не более 3.
4.5 (4.15). Напряжения в растянутой арматуре (или приращения напряжении) ss должны определяться по формулам для элементов:
изгибаемых
ss = 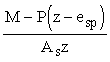 ; (66) ; (66)
внецентренно сжатых при еo,tot і 0,8ho
ss = 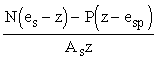 . (67) . (67)
В формулах (66) и (67) :
z - расстояние от центра тяжести площади сечения арматуры S до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной, определяемое согласно п. 4.7.
При расположении растянутой арматуры в несколько рядов по высоте сечения в изгибаемых и внецентренно сжатых элементах при еo,tot і 0,8ho напряжения ss, подсчитанные по формулам (66) и (67), должны умножаться на коэффициент dn, равный
dn = 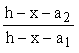 , (68) , (68)
где х = xho, значение определяется по формуле (70);
а1 и a2 - расстояния от центра тяжести площади сечения соответственно всей арматуры S и крайнего ряда стержней до наиболее растянутого волокна бетона.
Значение напряжения ss + ssp, а при многорядной растянутой арматуре dn ss + ssp не должно превышать Rs,ser. | 




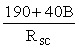 Ј 1 ;
Ј 1 ;
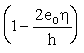 . (2)
. (2)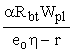 . (3)
. (3)
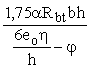 . (4)
. (4)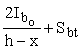 ; (5)
; (5)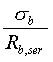 , (6)
, (6)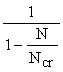 , (9)
, (9)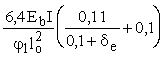 , (10)
, (10)
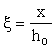 , определяемой из соответствующих условий равновесия, и значением относительной высоты сжатой зоны бетона (см. п. 3.13), при котором предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению Rs, с учетом соответствующих коэффициентов условий работы арматуры, за исключением коэффициента gs6 по п. 3.13 СНиП 2.03.01-84.
, определяемой из соответствующих условий равновесия, и значением относительной высоты сжатой зоны бетона (см. п. 3.13), при котором предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению Rs, с учетом соответствующих коэффициентов условий работы арматуры, за исключением коэффициента gs6 по п. 3.13 СНиП 2.03.01-84.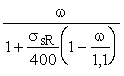 , (18)
, (18)
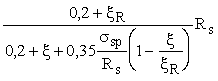 ; (23)
; (23)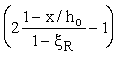 Rs ; (27)
Rs ; (27)
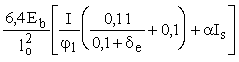 , (28)
, (28)
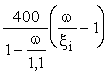 + sspi . (31)
+ sspi . (31)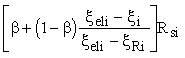 , (32)
, (32)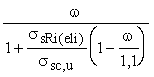 . (33)
. (33)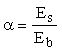 ;
; 
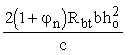 , (38)
, (38)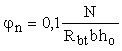 , но не более 0,5. (39)
, но не более 0,5. (39)
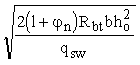 , (40)
, (40)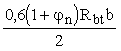 . (43)
. (43)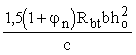 , (44)
, (44)
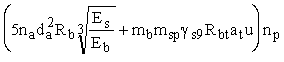 , (50)
, (50)





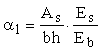 ;
; 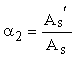 . (61)
. (61)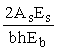 . (63)
. (63)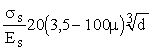 , (64)
, (64)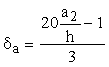 (65)
(65)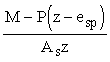 ; (66)
; (66)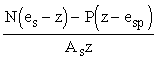 . (67)
. (67)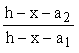 , (68)
, (68)
